Zunächst soll in einem etwas theoretischen Beitrag die 80/20-Verteilung betrachtet und diskutiert werden.
Aus der Überlieferung und der Archäologie ist bekannt, dass es im alten Mesopotamien vor etwa 5000 Jahren schon eine Schuldknechtschaft gab. Es existierte zwar noch kein Geld, aber die Schuldscheine (Rollsiegel mit Hieroglyphen) wurden auf Naturalien ausgestellt, zum Beispiel: „So und so viel Weizen – Rückzahlung bei der nächsten Ernte“. Wer nicht zurückzahlen konnte, musste in die Schuldknechtschaft. Irgendwann waren soviel Menschen in der Schuldknechtschaft, dass der mesopotamische König alle Schuldscheine für ungültig erklärte. Und das Spiel begann von vorn. Das Merkwürdige daran war, dass nach einer Zeitlang, sich ähnliche Besitzverhältnisse wieder herausgebildet hatten: auf der einen Seite, eine Menge von Leuten in der Schuldknechtschaft, auf der anderen Seite wenig Leute, die eine größere Menge an Schuldscheinen hielten.
Schon damals hätte man auf den Gedanken kommen können, dass sich hinter diesem Phänomen etwas Grundsätzliches, vielleicht ein Trend, vielleicht sogar ein Gesetz verbirgt. Der Ingenieur, Ökonom und Soziologe Vilfredo Pareto (1848−1923) untersuchte laut Angaben in der Literatur am Anfang des 20. Jahrhunderts (1906) die Vermögensverhältnisse in Italien. Dabei stellte er fest, dass rund 20 % der italienischen Familien etwa 80 % des Vermögens des Landes besaßen. Diese Vermögens-Verteilung war aber kein Zufall, denn in anderen europäischen Ländern war es ähnlich.
Übrigens, etwa zehn Jahre (1897) zuvor hatte Pareto eine Verteilung der Einkommen in Italien untersucht und war auf eine Funktion gestoßen, nach der diese Einkommensverteilung berechnet werden konnte:
Dabei ist Nx die Anzahl von Personen mit einem Einkommen von mindestens x Einheiten; x darf also nicht Null gesetzt werden, sondern hat einen Schwellenwert. Und A und α sind Parameter (positive Zahlen). Von dieser Formel wurde die Pareto-Verteilung abgeleitet, nach der statistische Probleme, wie in der Versicherung, bearbeitet werden. Aber das nur am Rande.
Paretos Entdeckung der ungleichen Vermögensverteilung sagt aber noch nichts über deren Ursache aus. Welcher Mechanismus wirkt, dass sich diese ungleiche Vermögens-Verteilung im Kapitalismus immer wieder einstellt? Selbst wenn man für einen Moment absolute Gleichheit in den Vermögen der Bürger oder Familien eines Landes herstellen würde, stellte sich nach einer Zeit eine ungleiche Vermögensverteilung dar (wie wir im eingangs erwähnten Fall von Mesopotamien, das noch kein Kapitalismus hatte, gesehen haben). Natürlich muss das mit den unterschiedlichen Einkommen der Bürger/Familien zusammenhängen. Um die Frage genauer zu untersuchen, schrieb ich ein Computerprogramm, bei dem ich eine Ursprungs-Einkommens-Verteilung mit folgenden Werten simulierte.
Betrachtet werden:
■ 5 Gesellschaftsmitglieder oder 5 Gesellschaftsgruppen (fünf wurde wegen der Quintile in der Pareto-Verteilung gewählt);
■ als Grundgehalt oder als Grundeinnahme soll jeder Gruppe 1000 (Euro oder Währungseinheiten) im Jahr bekommen;
■ die fünf Gesellschaftsgruppen unterscheiden sich dadurch, dass die Einkommen ab den 1000 Euro Grundeinkommen abgestuft sind, und zwar in 500er Einheiten. Die erste Gruppe bekommt also 1000 Einheiten, die zweite 1500 Einheiten, die dritte 2000 Einheiten, usw., bis zur fünften, die 3000 Einheiten erhält.
■ die Grundausgabe einer Gruppe ist hingegen 900 Einheiten;
■ wieder unterscheiden sich die Gruppen nach der Höhe der Ausgaben, und zwar diesmal in 250er Schritten. Die erste Gruppe gibt im Jahr 900 Einheiten aus, die zweite Gruppe 1150, die dritte Gruppe 1400 Einheiten, usw. und die fünfte Gruppe 1900 Einheiten, denn sie nimmt ja auch mehr ein, ganz nach dem Motto: „Wer mehr einnimmt, kann auch mehr ausgeben.“
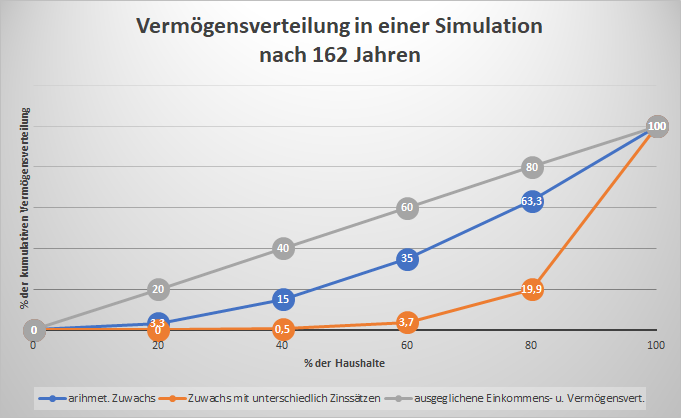
Nachdem das Grundgerüst der Simulation skizziert wurde, wird auf zwei grundlegende Betrachtungsweisen eingegangen (s. nachfolgende Grafik):
■ Zum ersten, der sogenannte arithmetische Zuwachs (blaue Linie in der Grafik). Alle obigen Annahmen gelten, es werden keine zusätzlichen Annahmen gemacht. (Der erste Wert in der blauen Kreisscheibe heißt 3,3 – schlecht lesbar, weil er sich mit der orangenen Kreisscheibe überschneidet.) Die blaue Linie stellt sich nach der Dauer von einem Jahr, 100 Jahren oder 200 Jahren so dar. Die Besonderheit ist also: Die Dauer spielt keine Rolle, die blaue Linie bleibt immer an derselben Position. Zwar ist das Vermögen der fünften Gruppe am höchsten, aber das spielt bei der Vermögens-Verteilung keine Rolle, weil auch das Vermögen der anderen Gruppen in den Jahren mitwächst, so dass die prozentuale Verteilung immer gleich bleibt. Ein Zustand, wie er etwa in der DDR bei der Vermögens-Verteilung charakteristisch war.
■ Zum zweiten, der Zuwachs mit unterschiedlichen Zinssätzen (orangene Linie in der Grafik). Alle obigen Annahmen gelten, aber es wird noch eine Annahme zusätzlich gemacht: das Vermögen, das sich bei den einzelnen gesellschaftlichen Gruppen bildet (Vermögen entsteht dadurch, dass bei allen Gruppen, nicht alles ausgeben wird, was eingenommen wird), soll sich mit einem unterschiedlichen Zinssatz jährlich erhöhen. Der Unterschied beträgt von Gruppe zu Gruppe 1 Prozent. Also bei der ersten Gruppe jährlich um 1 Prozent, bei der zweiten Gruppe jährlich um 2 Prozent, bei der dritten Gruppe jährlich um 3 Prozent, usw., bei der fünften Gruppe jährlich um 5 Prozent.
Ergebnis: Im ersten Jahr liegt die Vermögensverteilung noch sehr nahe an der blauen Linie, also an der arithmetischen und verändert sich erst allmählich im Laufe der Zeit. Bis sie nach 162 Jahren im fünften Quintil den Wert aus dem Pareto-Prinzip 80 % erreicht. Natürlich hängt diese Dauer von den gewählten Ausgangsdaten ab, und könnte bei veränderten Ausgangsdaten schneller den Wert von 80 % erreichen.
Schlussfolgerung:
Die Computer-Simulation bestätigt die Aussagen des französischen Ökonomen Thomas Piktetty, der Vermögensverteilung in Industrieländern in seinem Buch „Das Kapital im 21. Jahrhundert“ über zwei Jahrhunderte weg untersucht und zu dem Ergebnis kommt, dass in den letzten 200 Jahren eine in den Industrieländern Frankreich, England und Deutschland starke ungleiche Vermögensverteilung vorherrscht. Diese Vermögens-Verteilung ist zwar nicht immer gleich unterschiedlich – z.B. nimmt sie zwischen den Weltkriegen im 20. Jahrhundert ab –, aber sie kehrt seit den 70er Jahren auf das alte Niveau zurück. Piketty vermutet als Ursache dafür, dass die Rendite von Kapital im allgemeinen größer als das Wirtschaftswachstum ist. (Seine Formel r > g; „r“ steht für den englischen Begriff „rate of return“, der Buchstabe „g“ für „growth of economy“) Von der Rendite des Kapitals profitieren die Kapitalbesitzer, von dem Wirtschaftswachstum die Gehalts- und Lohnempfänger. Durch Vererbung von Vermögen, das fast ungeschmälert an nachfolgende Generationen weiter gereicht wird, ist der Kreis der Vermögensbesitzer in einer Gesellschaft ziemlich festgeschrieben. Die beschriebene Computer-Simulation bestätigt Pikettys Meinung insoweit, dass zu den großen Vermögensunterschieden nicht ein einfacher Einkommensunterschied beiträgt, sondern ein „Rendite-Effekt“ oder ein „Zinses-Zins-Effekt“ dahintersteckt.
Als Beleg, dass das Pareto-Prinzip auch heute noch bei der Vermögens-Verteilung wirkt, soll eine Grafik des Deutschen Instituts für Wirtschaftsforschung in Berlin angeführt werden, die die Vermögens-Verteilung in Deutschland 2014 aufzeigt.
Anmerkung: Zum Vermögen zählt dabei: Immobilien, Geldvermögen, private Versicherungen, Sachvermögen, wie Antiquitäten, Gold oder Kunstsammlungen und Betriebsvermögen. Hypotheken müssen abgezogen werden, ebenso Konsumentenkredite oder Studienkredite.
Wenn man die beiden letzten Dezentile der Grafik addiert, kommt man auf 78,86 % (also rund 78,9 %, man sollte sowieso die zweite Kommastelle runden, da es bei der Erfassung der Vermögensungleichheit durch die Begrenztheit des Ausgangs-Datenmaterials zu Ungenauigkeiten kommt, worauf der Verteilungsforscher Markus Grabka vom deutschen Institut für Wirtschaftsforschung in Berlin hinweist. Aber die Größenordnung der Aussagen stimmt, wie auch andere Studien belegen.)
Welche Schlussfolgerungen sich aus dem Bisherigen ergeben, soll in weiteren Beiträgen untersucht werden.